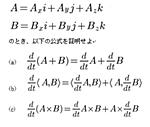id:moon-fondu
ポイントあり105ptベストアンサーあり
学習・教育

1276008268 解析幾何学や2次曲線の授業で出された課題なのですが・・・どのように証明すればよいのか困っています。


問題文は、添付ファイルをご覧いただければ幸いです。

そもそも何の公式なのかも、さっぱりわからない状態でして・・・(ToT)
皆様のお力をお貸しいただきたい次第です。
よろしくお願いします<m(__)m>

回答の条件
  • 1人5回まで
  • 登録：
  • 終了：2010/06/14 21:47:33
※ 有料アンケート・ポイント付き質問機能は2023年2月28日に終了しました。

ベストアンサー

id:rsc96074 No.2

回答回数4503ベストアンサー獲得回数437

ポイント100pt

　ｉ,ｊ,ｋは、高校流に表せば、↑ｅ_x,↑ｅ_y,↑ｅ_zです。

Ａ＝Ａxｉ＋Ａyｊ＋Ａzｋ　を成分で表せば、　Ａ＝(Ａx,Ａy,Ａz)

Ｂ＝Ｂxｉ＋Ｂyｊ＋Ｂzｋ　を成分で表せば、　Ｂ＝(Ｂx,Ｂy,Ｂz)

　ベクトル ↑ｕを大文字のＵ一文字で表すことにすると、まず、基本公式として、一般に、

　ベクトルＵ＝(x,y,x) の各成分が実数 t の関数であるとき，

　dＵ/dt＝(dx/dt,dy/dt,dz/dt)

※1番目のURL参照。あるいは、2番目のURLの(33)式（7ページ目）参照。

(1)方針としては、成分で表して、証明します。行数節約のため、行ベクトルで表しますが、自分で紙に書くときは列ベクトルにすると見やすいです。それから、たとえば、(d/dt)Ａx＝Ａx'で表すことにします。

　Ａ＋Ｂ＝(Ａx＋Ｂx,Ａy＋Ｂy,Ａz＋Ｂz)

∴

(左辺)＝(d/dt)(Ａ＋Ｂ)

＝（(d/dt)(Ａx＋Ｂx),(d/dt)(Ａy＋Ｂy),(d/dt)(Ａz＋Ｂz)）

＝（Ａx'＋Ｂx',Ａy'＋Ｂy',Ａz'＋Ｂz'）・・・①

(右辺)＝(d/dt)Ａ＋(d/dt)Ｂ

＝（Ａx',Ａy',Ａz'）＋（Ｂx',Ｂy',Ｂz'）

＝（Ａx'＋Ｂx',Ａy'＋Ｂy',Ａz'＋Ｂz'）・・・②

　①,②から、

∴(d/dt)(Ａ＋Ｂ)＝(d/dt)Ａ＋(d/dt)Ｂ

(2)<Ａ, Ｂ> は Ａ と Ｂ の内積を表すようです。

<Ａ, Ｂ>＝ＡxＢx＋ＡyＢy＋ＡzＢz　←スカラーになっています。

Ａx,Ｂx,Ａy,Ｂy,Ａz,Ｂzは、ｔの関数で、積の微分法を用いて、

∴

(左辺)＝(d/dt)<Ａ, Ｂ>

＝(Ａx'Ｂx＋ＡxＢx')＋(Ａy'Ｂy＋ＡyＢy')＋(Ａz'Ｂz＋ＡzＢz')

＝(Ａx'Ｂx＋Ａy'Ｂy＋Ａz'Ｂz)＋(ＡxＢx'＋ＡyＢy'＋ＡzＢz')・・・③

<(d/dt)Ａ, Ｂ>＝Ａx'Ｂx＋Ａy'Ｂy＋Ａz'Ｂz・・・④

<Ａ, (d/dt)Ｂ>＝ＡxＢx'＋ＡyＢy'＋ＡzＢz'・・・⑤

　③,④,⑤から、

∴(d/dt)<Ａ, Ｂ>＝<(d/dt)Ａ, Ｂ>＋<Ａ, (d/dt)Ｂ>

※2番目のURLの7ページ目の方法（(35)式）でもいいです。

(3)方針としては、成分で表して、証明します。

Ａ×Ｂ＝|ｉ   ｊ   ｋ |
      |Ａx  Ａy  Ａz|
      |Ｂx  Ｂy  Ｂz|
＝（ＡyＢz-ＡzＢy）ｉ＋（ＡzＢx-ＡxＢz）ｊ＋（ＡxＢy-ＡyＢx）ｋ

∴成分で表すと

Ａ×Ｂ＝（ＡyＢz-ＡzＢy,ＡzＢx-ＡxＢz,ＡxＢy-ＡyＢx）・・・⑥

同様にして、

(d/dt)Ａ×Ｂ＝（Ａy'Ｂz-Ａz'Ｂy,Ａz'Ｂx-Ａx'Ｂz,Ａx'Ｂy-Ａy'Ｂx）・・・⑦

Ａ×(d/dt)Ｂ＝（ＡyＢz'-ＡzＢy',ＡzＢx'-ＡxＢz',ＡxＢy'-ＡyＢx'）・・・⑧

∴

　⑥から、

(左辺)＝(d/dt)(Ａ×Ｂ)

＝（(d/dt)(ＡyＢz-ＡzＢy),(d/dt)(ＡzＢx-ＡxＢz),(d/dt)(ＡxＢy-ＡyＢx)）

　ｘ成分について、Ａy,Ａz,Ｂy,Ｂzは、ｔの関数で、積の微分法から、

(d/dt)(ＡyＢz-ＡzＢy)＝Ａy'Ｂz＋ＡyＢz'－Ａz'Ｂy－ＡzＢy'

＝(Ａy'Ｂz－Ａz'Ｂy)＋(ＡyＢz'－ＡzＢy')・・・⑨

　ｙ成分について、同様にして、

(d/dt)(ＡzＢx-ＡxＢz)＝Ａz'Ｂx＋ＡzＢx'－Ａx'Ｂz－ＡxＢz'

＝(Ａz'Ｂx－Ａx'Ｂz)＋(ＡzＢx'－ＡxＢz')・・・⑩

　ｚ成分について、同様にして、

(d/dt)(ＡxＢy-ＡyＢx)＝Ａx'Ｂy＋ＡxＢy'－Ａy'Ｂx－ＡyＢx'

＝(Ａx'Ｂy－Ａy'Ｂx)＋(ＡxＢy'－ＡyＢx')・・・⑪

　⑦,⑧から、

(右辺)＝(d/dt)Ａ×Ｂ＋Ａ×(d/dt)Ｂ

＝（Ａy'Ｂz-Ａz'Ｂy,Ａz'Ｂx-Ａx'Ｂz,Ａx'Ｂy-Ａy'Ｂx）＋（ＡyＢz'-ＡzＢy',ＡzＢx'-ＡxＢz',ＡxＢy'-ＡyＢx'）

＝（(Ａy'Ｂz-Ａz'Ｂy)+(ＡyＢz'-ＡzＢy'),(Ａz'Ｂx-Ａx'Ｂz)+(ＡzＢx'-ＡxＢz'),(Ａx'Ｂy-Ａy'Ｂx)+(ＡxＢy'-ＡyＢx')）・・・⑫

⑨,⑩,⑪,⑫から、

∴(d/dt)(Ａ×Ｂ)＝(d/dt)Ａ×Ｂ＋Ａ×(d/dt)Ｂ

※参考URL

●ベクトルと微分

http://aozoragakuen.sakura.ne.jp/kaisekikiso/node68.html

●1 ベクトル

http://docs.google.com/viewer?a=v&q=cache:MEXoFSsnLs4J:www-het.p...

http://www-het.phys.sci.osaka-u.ac.jp/~higashij/lecture/am03/vec...

●数学記号の表

　<x, y> は x と y の内積を表す

http://ja.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6%E8%A8%98%E5%8F%B...

●ベクトルの演算（4）

＞ベクトルの内積の微分

http://www.geocities.jp/newtondynam/sugaku/vecten4.html

●外積と微分

http://members.ld.infoseek.co.jp/aozora_m/taiwa2/inryoku/node12....

http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1136477...

id:moon-fondu

なるほどです、1番目と2番目のURL、参考にさせていただきました！

「ベクトルの微分」なるものを使えば、証明できるそうで。そして、

■□■□■□■□■□

ベクトルＵ＝(x,y,z) の各成分が実数 t の関数であるとき，

dＵ/dt＝(dx/dt,dy/dt,dz/dt)

■□■□■□■□■□

が、ベクトルの微分の基本公式ですね！

列ベクトルは、

　　　　(Ａx＋Ｂx)

Ａ＋Ｂ＝(Ａy＋Ｂy)

　　　　(Ａz＋Ｂz)

な感じですよね、レイアウトが崩れちゃいやすい感じの・・・(^_^;)

(1)は、基本公式を普通に当てはめれば証明出来るみたいで。

(2)は、そうなんです、山カッコが何を意味しているのか判然としてなかったのですが・・・リンク先の「数学記号の表」拝見しました！rsc96074さんはリサーチ力もすごいですね(TωT)

ここでちょっと詰まりましたが、「2番目のURLの7ページ目の方法（(35)式）」を拝見すると、「ベクトルの積を微分するときも、積の微分法の公式(24)を用いればよい。」と書かれてあったのが参考になりました！

(f(x)g(x))'= f'(x)g(x) + f(x)g'(x)

は、ベクトルの積にも使えるんですね～。

(3)は、(2)を複雑にした感じですね。

でもなんとなく理解できました、ありがとうございます！

ただ、一つだけ疑問が残りまして。

(3)で、rsc96074さんが一番最初に書いてくださった、

Ａ×Ｂ＝|ｉ ｊ ｋ |

|Ａx Ａy Ａz|

|Ｂx Ｂy Ｂz|

＝（ＡyＢz-ＡzＢy）ｉ＋（ＡzＢx-ＡxＢz）ｊ＋（ＡxＢy-ＡyＢx）ｋ

についてなのですが、どうして一行目にi、j、kと、出てきているのでしょうか？

そもそも、AとBを掛け合わせたものが「三行三列の行列でも表せる」という根拠を、問題文のうちのどこに見出せばよいのでしょうか？AもBも、項が3つあるからでしょうか？

すごく当たり前のことを聞いているかもしれず、申し訳ないのですが、再度ご回答いただければ幸いです。

よろしくお願いします(>_<)

2010/06/12 01:47:46

その他の回答（1件）

id:koriki-kozou No.1

回答回数480ベストアンサー獲得回数79

ポイント5pt

ベクトルの公式証明問題のようだね

左辺／右辺のどちらからでもいいから、成分をあらわす式（例えば {d(AxBx+AyBy+AzBz) \over dt} な感じ）にどんどん置き換えていけば辿り付くよ

課題は自分で解かないと意味無いから、この先は講義で使ったテキストやプリント、ノートを読み直して

（「ベクトル　公式」で検索してもいいけどね。検索して検証したならば自力で調べたと言えるし、スキルアップにもなるしね）

id:moon-fondu

そうですよね・・・でも、自力で解ける水準になるには、多くの問題をインプットしておかないと難しい気もするので・・・講義で使ったテキストやプリントはあまり当てにならないので・・・いつもここに甘えてます・・・(^_^;)

2010/06/12 01:49:15
id:rsc96074 No.2

回答回数4503ベストアンサー獲得回数437ここでベストアンサー

ポイント100pt

　ｉ,ｊ,ｋは、高校流に表せば、↑ｅ_x,↑ｅ_y,↑ｅ_zです。

Ａ＝Ａxｉ＋Ａyｊ＋Ａzｋ　を成分で表せば、　Ａ＝(Ａx,Ａy,Ａz)

Ｂ＝Ｂxｉ＋Ｂyｊ＋Ｂzｋ　を成分で表せば、　Ｂ＝(Ｂx,Ｂy,Ｂz)

　ベクトル ↑ｕを大文字のＵ一文字で表すことにすると、まず、基本公式として、一般に、

　ベクトルＵ＝(x,y,x) の各成分が実数 t の関数であるとき，

　dＵ/dt＝(dx/dt,dy/dt,dz/dt)

※1番目のURL参照。あるいは、2番目のURLの(33)式（7ページ目）参照。

(1)方針としては、成分で表して、証明します。行数節約のため、行ベクトルで表しますが、自分で紙に書くときは列ベクトルにすると見やすいです。それから、たとえば、(d/dt)Ａx＝Ａx'で表すことにします。

　Ａ＋Ｂ＝(Ａx＋Ｂx,Ａy＋Ｂy,Ａz＋Ｂz)

∴

(左辺)＝(d/dt)(Ａ＋Ｂ)

＝（(d/dt)(Ａx＋Ｂx),(d/dt)(Ａy＋Ｂy),(d/dt)(Ａz＋Ｂz)）

＝（Ａx'＋Ｂx',Ａy'＋Ｂy',Ａz'＋Ｂz'）・・・①

(右辺)＝(d/dt)Ａ＋(d/dt)Ｂ

＝（Ａx',Ａy',Ａz'）＋（Ｂx',Ｂy',Ｂz'）

＝（Ａx'＋Ｂx',Ａy'＋Ｂy',Ａz'＋Ｂz'）・・・②

　①,②から、

∴(d/dt)(Ａ＋Ｂ)＝(d/dt)Ａ＋(d/dt)Ｂ

(2)<Ａ, Ｂ> は Ａ と Ｂ の内積を表すようです。

<Ａ, Ｂ>＝ＡxＢx＋ＡyＢy＋ＡzＢz　←スカラーになっています。

Ａx,Ｂx,Ａy,Ｂy,Ａz,Ｂzは、ｔの関数で、積の微分法を用いて、

∴

(左辺)＝(d/dt)<Ａ, Ｂ>

＝(Ａx'Ｂx＋ＡxＢx')＋(Ａy'Ｂy＋ＡyＢy')＋(Ａz'Ｂz＋ＡzＢz')

＝(Ａx'Ｂx＋Ａy'Ｂy＋Ａz'Ｂz)＋(ＡxＢx'＋ＡyＢy'＋ＡzＢz')・・・③

<(d/dt)Ａ, Ｂ>＝Ａx'Ｂx＋Ａy'Ｂy＋Ａz'Ｂz・・・④

<Ａ, (d/dt)Ｂ>＝ＡxＢx'＋ＡyＢy'＋ＡzＢz'・・・⑤

　③,④,⑤から、

∴(d/dt)<Ａ, Ｂ>＝<(d/dt)Ａ, Ｂ>＋<Ａ, (d/dt)Ｂ>

※2番目のURLの7ページ目の方法（(35)式）でもいいです。

(3)方針としては、成分で表して、証明します。

Ａ×Ｂ＝|ｉ   ｊ   ｋ |
      |Ａx  Ａy  Ａz|
      |Ｂx  Ｂy  Ｂz|
＝（ＡyＢz-ＡzＢy）ｉ＋（ＡzＢx-ＡxＢz）ｊ＋（ＡxＢy-ＡyＢx）ｋ

∴成分で表すと

Ａ×Ｂ＝（ＡyＢz-ＡzＢy,ＡzＢx-ＡxＢz,ＡxＢy-ＡyＢx）・・・⑥

同様にして、

(d/dt)Ａ×Ｂ＝（Ａy'Ｂz-Ａz'Ｂy,Ａz'Ｂx-Ａx'Ｂz,Ａx'Ｂy-Ａy'Ｂx）・・・⑦

Ａ×(d/dt)Ｂ＝（ＡyＢz'-ＡzＢy',ＡzＢx'-ＡxＢz',ＡxＢy'-ＡyＢx'）・・・⑧

∴

　⑥から、

(左辺)＝(d/dt)(Ａ×Ｂ)

＝（(d/dt)(ＡyＢz-ＡzＢy),(d/dt)(ＡzＢx-ＡxＢz),(d/dt)(ＡxＢy-ＡyＢx)）

　ｘ成分について、Ａy,Ａz,Ｂy,Ｂzは、ｔの関数で、積の微分法から、

(d/dt)(ＡyＢz-ＡzＢy)＝Ａy'Ｂz＋ＡyＢz'－Ａz'Ｂy－ＡzＢy'

＝(Ａy'Ｂz－Ａz'Ｂy)＋(ＡyＢz'－ＡzＢy')・・・⑨

　ｙ成分について、同様にして、

(d/dt)(ＡzＢx-ＡxＢz)＝Ａz'Ｂx＋ＡzＢx'－Ａx'Ｂz－ＡxＢz'

＝(Ａz'Ｂx－Ａx'Ｂz)＋(ＡzＢx'－ＡxＢz')・・・⑩

　ｚ成分について、同様にして、

(d/dt)(ＡxＢy-ＡyＢx)＝Ａx'Ｂy＋ＡxＢy'－Ａy'Ｂx－ＡyＢx'

＝(Ａx'Ｂy－Ａy'Ｂx)＋(ＡxＢy'－ＡyＢx')・・・⑪

　⑦,⑧から、

(右辺)＝(d/dt)Ａ×Ｂ＋Ａ×(d/dt)Ｂ

＝（Ａy'Ｂz-Ａz'Ｂy,Ａz'Ｂx-Ａx'Ｂz,Ａx'Ｂy-Ａy'Ｂx）＋（ＡyＢz'-ＡzＢy',ＡzＢx'-ＡxＢz',ＡxＢy'-ＡyＢx'）

＝（(Ａy'Ｂz-Ａz'Ｂy)+(ＡyＢz'-ＡzＢy'),(Ａz'Ｂx-Ａx'Ｂz)+(ＡzＢx'-ＡxＢz'),(Ａx'Ｂy-Ａy'Ｂx)+(ＡxＢy'-ＡyＢx')）・・・⑫

⑨,⑩,⑪,⑫から、

∴(d/dt)(Ａ×Ｂ)＝(d/dt)Ａ×Ｂ＋Ａ×(d/dt)Ｂ

※参考URL

●ベクトルと微分

http://aozoragakuen.sakura.ne.jp/kaisekikiso/node68.html

●1 ベクトル

http://docs.google.com/viewer?a=v&q=cache:MEXoFSsnLs4J:www-het.p...

http://www-het.phys.sci.osaka-u.ac.jp/~higashij/lecture/am03/vec...

●数学記号の表

　<x, y> は x と y の内積を表す

http://ja.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6%E8%A8%98%E5%8F%B...

●ベクトルの演算（4）

＞ベクトルの内積の微分

http://www.geocities.jp/newtondynam/sugaku/vecten4.html

●外積と微分

http://members.ld.infoseek.co.jp/aozora_m/taiwa2/inryoku/node12....

http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1136477...

id:moon-fondu

なるほどです、1番目と2番目のURL、参考にさせていただきました！

「ベクトルの微分」なるものを使えば、証明できるそうで。そして、

■□■□■□■□■□

ベクトルＵ＝(x,y,z) の各成分が実数 t の関数であるとき，

dＵ/dt＝(dx/dt,dy/dt,dz/dt)

■□■□■□■□■□

が、ベクトルの微分の基本公式ですね！

列ベクトルは、

　　　　(Ａx＋Ｂx)

Ａ＋Ｂ＝(Ａy＋Ｂy)

　　　　(Ａz＋Ｂz)

な感じですよね、レイアウトが崩れちゃいやすい感じの・・・(^_^;)

(1)は、基本公式を普通に当てはめれば証明出来るみたいで。

(2)は、そうなんです、山カッコが何を意味しているのか判然としてなかったのですが・・・リンク先の「数学記号の表」拝見しました！rsc96074さんはリサーチ力もすごいですね(TωT)

ここでちょっと詰まりましたが、「2番目のURLの7ページ目の方法（(35)式）」を拝見すると、「ベクトルの積を微分するときも、積の微分法の公式(24)を用いればよい。」と書かれてあったのが参考になりました！

(f(x)g(x))'= f'(x)g(x) + f(x)g'(x)

は、ベクトルの積にも使えるんですね～。

(3)は、(2)を複雑にした感じですね。

でもなんとなく理解できました、ありがとうございます！

ただ、一つだけ疑問が残りまして。

(3)で、rsc96074さんが一番最初に書いてくださった、

Ａ×Ｂ＝|ｉ ｊ ｋ |

|Ａx Ａy Ａz|

|Ｂx Ｂy Ｂz|

＝（ＡyＢz-ＡzＢy）ｉ＋（ＡzＢx-ＡxＢz）ｊ＋（ＡxＢy-ＡyＢx）ｋ

についてなのですが、どうして一行目にi、j、kと、出てきているのでしょうか？

そもそも、AとBを掛け合わせたものが「三行三列の行列でも表せる」という根拠を、問題文のうちのどこに見出せばよいのでしょうか？AもBも、項が3つあるからでしょうか？

すごく当たり前のことを聞いているかもしれず、申し訳ないのですが、再度ご回答いただければ幸いです。

よろしくお願いします(>_<)

2010/06/12 01:47:46

コメント（3件)

  • id:rsc96074
    rsc 2010/06/09 08:47:22
    　すみません。書き間違いがありました。
    ＞　ベクトルＵ＝(x,y,x) の各成分が・・・
    正しくは、
    　　ベクトルＵ＝(x,y,z) の各成分が・・・
  • id:rsc96074
    rsc 2010/06/12 09:46:25
    　もしかしたら、深い意味があるのかも知れませんが、これは、計算結果がそうなっているというだけで、形が憶えやすいので形式的な公式の記憶法的なものだと思っていました。(^_^;

    ●[DOC] 外積（ベクトル積）　←2ページ目参照
    http://www.ge.kochi-ct.ac.jp/~hori/gaiseki.doc
    http://webcache.googleusercontent.com/search?q=cache:90cEwzqDpBYJ:www.ge.kochi-ct.ac.jp/~hori/gaiseki.doc+%E5%A4%96%E7%A9%8D+%E8%A1%8C%E5%88%97%E5%BC%8F&cd=5&hl=ja&ct=clnk&gl=jp
  • id:moon-fondu
    moon-fondu 2010/06/14 21:46:55
    ありがとうございます。
    外積に、

    a×b＝|ｉ ｊ ｋ |

    　　　　|a1 a2 a3|

    　　　　|b1 b2 b3|


    という定義があったなんて知りませんでした！

    添付ファイルを拝見したのですが、外積について、わからないところがありまして・・・・
    ここ↓
    http://q.hatena.ne.jp/1276519568
    に、新たな質問を立ち上げましたので、もしよろしければ、ご指導いただければ幸いです。
    よろしくお願いします(>_<)

この質問への反応（ブックマークコメント）

「あの人に答えてほしい」「この質問はあの人が答えられそう」というときに、回答リクエストを送ってみてましょう。

これ以上回答リクエストを送信することはできません。制限について

回答リクエストを送信したユーザーはいません
ユーザー登録をして使いはじめる!無料
すでに登録されている方はこちらからログイン
この質問に含まれるキーワード
知りたいことを検索してみよう
▲ページトップへ