 等比数列の和の公式の導き方に納得できない箇所があるのですが、教えてください。まずは添付画像をご覧になってください。
等比数列の和の公式の導き方に納得できない箇所があるのですが、教えてください。まずは添付画像をご覧になってください。
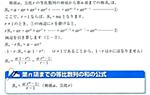
画像は、第N項までの等比数列の和の公式です。
わからないのは以下の2点です。
1,4行目に「…①の両辺にrを掛けると」と記載されていますが、どうして両辺にrを掛ける必要があるのでしょうか。
2,最後の行(青い枠の一歩前の行)に、1-rがr-1に変形されていますが、どうやって1-rがr-1に変形したのかがわかりません。(初歩的な質問ですいません(^^;))
以上2点ですが、一部の回答でもかまいませんのでよろしくお願いいたします。
 120pt
120pt
>1、どうして両辺にrを掛ける必要があるのでしょうか。
(2)の式を作るためです。
なぜ(2)の式を作る必要があるかというと、(1)の式と両辺を引き算して間のたくさんの項を消したいからです。
(1)の式と(2)の式を引き算する、というのを詳しく書くと以下のようになります。
Sn - rSn = (a + ar + ar^2 + ar^3 ... + ar^n-1) - (ar + ar^2 + ar^3 + ar^4 ... + ar^n)
= a + ar + ar^2 + ar^3 ... + ar^n-1 - ar - ar^2 - ar^3 - ar^4 ... - ar^n
= a + (ar - ar) + (ar^2 - ar^2) + (ar^3 - ar^3) + ... + (ar^n-1 - ar^n-1) - ar^n
= a - ar^n
指数の n の部分が1つずつずれて互いに消しあい、頭とおしりの a と ar^n だけが上手く残って式がきれいになったのがわかります。
>2、最後の行でどうやって1-rがr-1に変形したのかがわかりません。
これは分母と分子の両方に -1 をかけただけです。丁寧に書くと以下のような感じです。
a(r^n - 1) -a(r^n - 1) a(-r^n + 1) a(1 - r^n)
Sn = ---------- = ----------- = ----------- = ----------
1 - r -(1 - r) -1 + r r - 1
わかりましたでしょうか?
ありがとうございました。とても詳細な説明で上手く理解できました。
たくさんの項を消すためにrを掛けたのですね。消した後残ったのがa-ar^nだけになると。1つずつずらすので、どんどん消えていくという手品だったのですね。
2番目のは-1を掛けた結果1-rがr-1となったんですね。詳しく解説してくださってありがとうございました。
回答ありがとうございます。
画像の教科書の説明よりも、
http://www2.kumagaku.ac.jp/teacher/~sasayama/macroecon/mailmagas...
の説明の方が役に立ちました。
預金の信用創造について無限等比級数の和を勉強していたのですが、上記ページにて有限等比級数の和の公式についても書かれており助かりました。