メネラウスの定理の証明について、質問があります。
-------------------
△ABCの辺AB、BC、CAの延長線と、頂点A、B、Cを通らない直線LMNと交わるとき、
BL/LC・CM/MA・AN/NB＝1
となることを証明せよ。
-------------------
という問題を解きたいのですが、普通のメネラウスの定理の証明とは違うようでして。。。
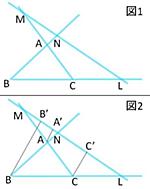
図が2つあります。図2は、ヒントだと思われます。
射影幾何学についての項目に記載されていた問題なので、それを使わないといけないのかもしれません・・・皆様のお力をお貸しいただきたい次第です。
よろしくお願いします(>_<)
No.1
4503
437
100pt
(BL/LC)･(CM/MA)･(AN/NB)＝1を証明したいのだから、左辺の(BL/LC)、(CM/MA)、(AN/NB)をそれぞれ他のもので表してみる方針。
図2のように、直線LMに垂線AA'、BB'、CC'を引くと、
BB'//CC'だから、△LBB'∽△LCC' （ただし、「∽」は相似記号）
∴BL/CL=BB'/CC'・・・①
CC'//AA'だから、△MCC'∽△MAA'
∴CM/AM=CC'/AA'・・・②
AA'//BB'だから、△NAA'∽△NBB'
∴AN/BN=AA'/BB'・・・③
①,②,③の辺々をかけて、
(BL/CL)(CM/AM)(AN/BN)=(BB'/CC')(CC'/AA')(AA'/BB')=1
辺の向きを整えて、
(BL/LC)(CM/MA)(AN/NB)=1
236
235
2
1
1
①の時点で一瞬「あれ？」と思いましたが、「BB':CC'=BL:CL→BB'･CL=BL･CC'」から、①も成り立ちんですね～(^_^;)
いやはや、ありがとうございます<m(__)m>