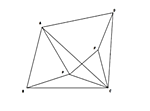
図のように、鋭角三角形ABCの内部の点をPとし、ACを一辺とする正三角形ACDと、CPを一辺とする正三角形CPP'をつくる。このとき、次の問いに応えなさい。
⑴PA=４㎝、PB=3㎝、PC=2㎝であるとき、折れ線BPP'Dの長さを求めよ。
⑵△ABCの内部に点Qをとって、QA+QB+QCの長さが最も短くなるとき、∠BQC,∠AQCの大きさをそれぞれ求めよ。
⑵について、基本的なことなんですが、「QA＋QB+QCの長さが最短になるのは4点B,Q,Q',Dが一直線に並ぶ場合」になぜ最短距離になるんでしょうか？
ご教示よろしくお願いします<(_ _)>
No.1
4974
2154
△APC と △DP'C が合同だ、っていうのを (1) も (2) も使うんでしょ。
(2) の場合は、(1) の P を Q に置き換えて考えて、
QA = DQ' ：△APC と △DP'C が合同だから
QC = QQ' ：△CQQ' が正三角形になるように Q' を取ったから
で、
QA + QB + QC
= DQ' + QB + QQ' ：QA = DQ' 、QC = QQ' を代入
= BQ + QQ' + Q'D ：並べ替え
これって、折れ線 BQQ'D の長さ。
B と D の位置は変わらないから、この折れ線が一番短くなるときは、BD の最短距離ということで、折れ線 BQQ'D が直線になるときが QA + QB + QC が一番短くなるとき。
3
1
1
1
2
1
2
0
コメント（0件)